A positive combinatorial formula for symplectic Kostka-Foulkes polynomials I: Rows

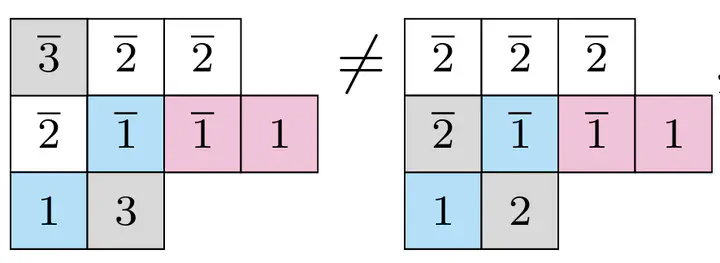
Abstract

We prove a conjecture of Lecouvey, which proposes a closed, positive combinatorial formula for symplectic Kostka-Foulkes polynomials, in the case of rows of arbitrary weight. To show this, we construct a new algorithm for computing cocyclage in terms of which the conjecture is described. Our algorithm is free of local constraints, which were the main obstacle in Lecouvey’s original construction. In particular, we show that our model is governed by the situation in type A. This approach works for arbitrary weight and we expect it to lead to a proof of the conjecture in full generality.